Dimension reduction is applied when there are large numbers of input features or fields, eithere becasue they are beleived to be correlated, or because the number is too large to be useful. In the case of numeric fields, the fields can be regarded as defining an N-dimensional space and the goal is to map this into an R-dimensional space where R is a lot smaller than N. An example is principal components analysis for numeric data that is assumed to have linear characteristics. Dimension reduction may also be applied to internal layers of a deep neural network to improve generalisation or simply reduse the size of the network to run faster or less powerful processors.
Defined on page 159
Used on pages 155, 158, 159, 189, 574
Also known as dimensional reduction, dimensionality reduction
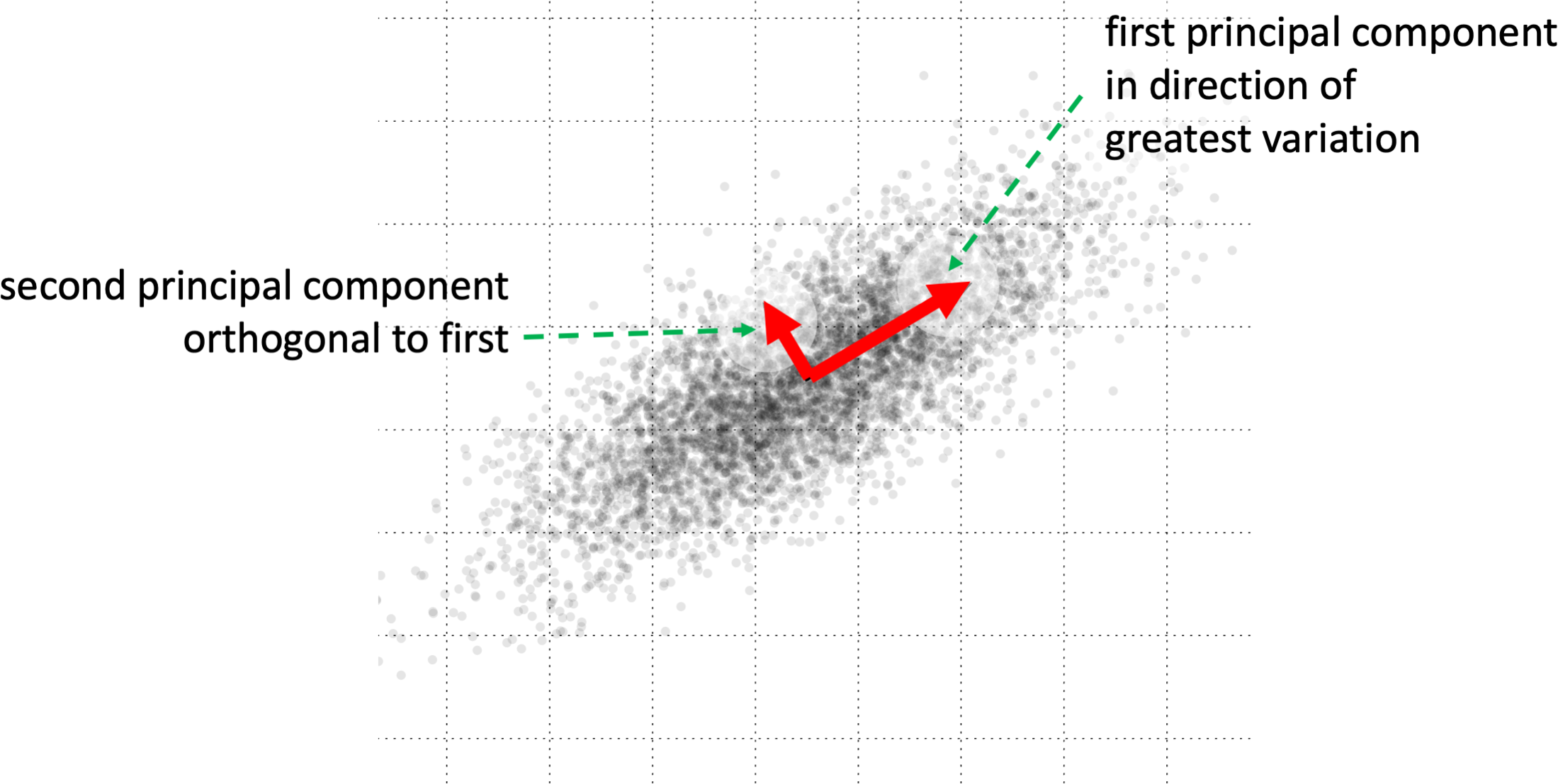
Principal components showing directions of maximum variation in the data set. (Adapted from Nicoguaro, CC BY 4.0, via Wikimedia Commons)
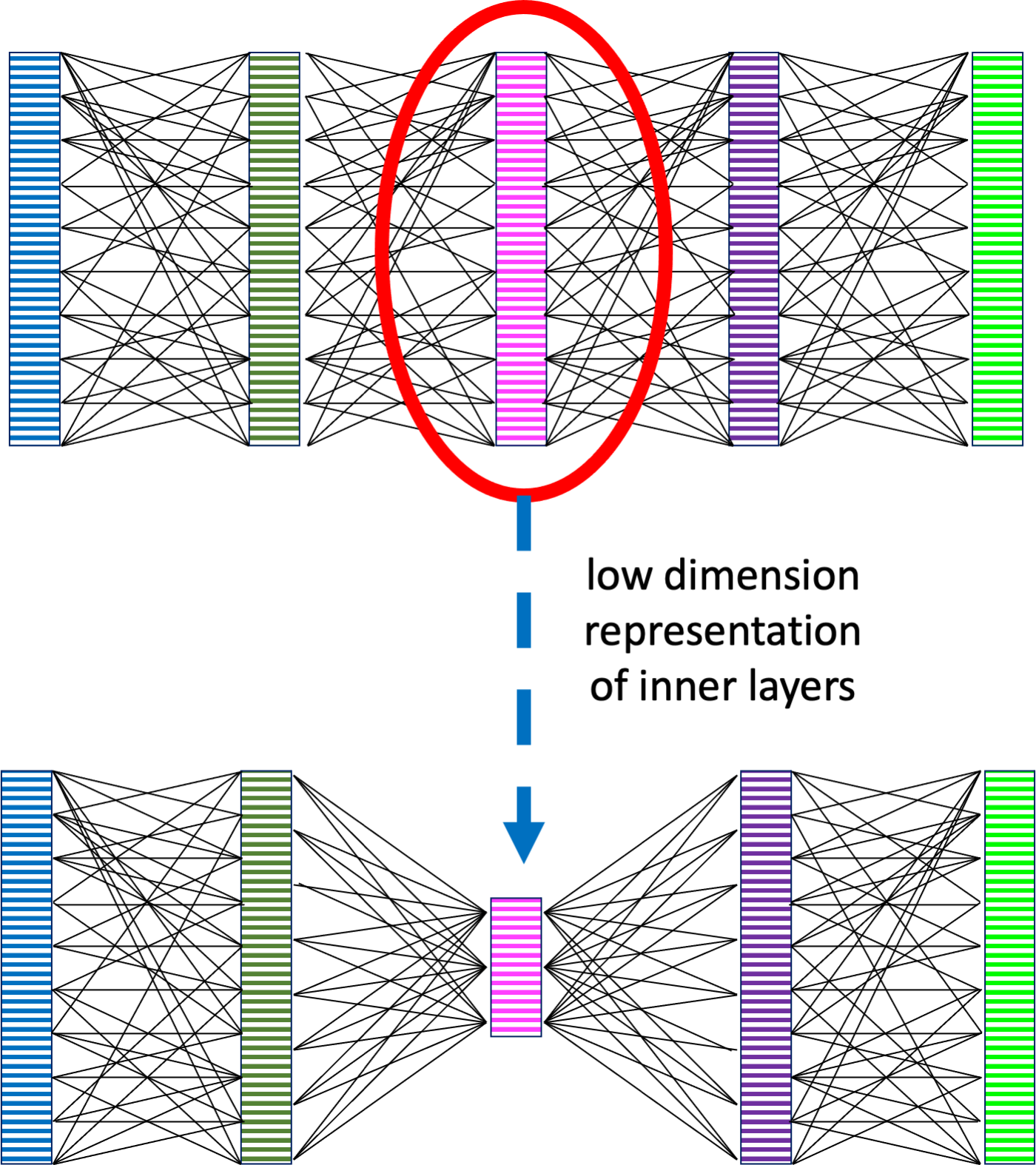
Reducing the dimensionality of inner layers to reduce re-training and runtime costs